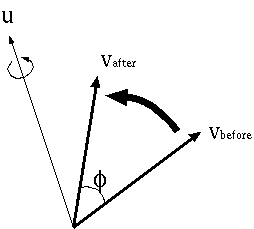
rotate
To calculate the components of the rotated vector of v around vector u by phi[rad] in right-handed screw rule, use the following code. v_after =rotate(v_before, vt2q(u, phi));
![\[ \overrightarrow{v}_\mathrm{after} =\mathbf{R}(\overrightarrow{u}, \phi) \overrightarrow{v}_\mathrm{before} \overline{\mathbf{R}(\overrightarrow{u}, \phi)} \]](form_8.png)
where 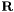 is
is
![\[ \mathbf{R}(\overrightarrow{u}, \phi) = \left[ \frac{{u_x}}{|\vec{u}|}\sin \left( \frac{\phi}{2} \right), \frac{{u_y}}{|\vec{u}|}\sin \left( \frac{\phi}{2} \right), \frac{{u_z}}{|\vec{u}|}\sin \left( \frac{\phi}{2} \right); \cos \left( \frac{\phi}{2} \right) \right] \]](form_10.png)
Generated on Tue Mar 15 16:02:38 2005 for QVM by
 1.4.1
1.4.1

![\[ \overrightarrow{v}_\mathrm{after} =\mathbf{R}(\overrightarrow{u}, \phi) \overrightarrow{v}_\mathrm{before} \overline{\mathbf{R}(\overrightarrow{u}, \phi)} \]](form_8.png)
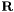 is
is ![\[ \mathbf{R}(\overrightarrow{u}, \phi) = \left[ \frac{{u_x}}{|\vec{u}|}\sin \left( \frac{\phi}{2} \right), \frac{{u_y}}{|\vec{u}|}\sin \left( \frac{\phi}{2} \right), \frac{{u_z}}{|\vec{u}|}\sin \left( \frac{\phi}{2} \right); \cos \left( \frac{\phi}{2} \right) \right] \]](form_10.png)
 1.4.1
1.4.1